
In other words, every NFA has a corresponding DFA which recognizes precisely the same language. The interested reader who lacks mathematical maturity would find it very accessible.) And Sisper’s book is much better than this terse post for a primer in Computing Theory. (We hate to refer the reader to an expensive textbook, but we could only find sparse proofs of this equivalence elsewhere on the internet, and most assume a particular working set of notation. This would be an appropriate exercise for the advanced reader, but the beginning student should see Sisper’s Introduction to the Theory of Computation, which contains a complete and thorough proof. Then, we can simulate any alphabet by the appropriate subset of $ \left \$ states, one corresponding to each subset of $ S$, and build up a deterministic transition function that makes things work. Since $ \Sigma$ is finite, we may assign to each element a unique finite string of ones and zeros (to keep things simple, let each string have length equal to ceiling of $ \log |\Sigma|)$. We will henceforth let inputs to our model be elements of $ \Sigma^*$ for some fixed alphabet $ \Sigma$, and operate on each character one at a time. We include the empty string $ \varepsilon$ as the string of zero length. This operation is called the Kleene star. This motivates the following two definitions:ĭefinition: An alphabet is a finite set, usually denoted $ \Sigma$.ĭefinition: $ \Sigma^*$ is the set of finite strings whose characters come from $ \Sigma$. Instead, we need to rigorously define the innards of our model for computation, and then see what kinds of things it can do.īecause our inputs may be long and complicated, our model should break an input into pieces and work on the pieces in sequence. We cannot learn anything interesting about computations if they are performed behind an opaque veil. Of course (assuming the winning numbers are chosen randomly), this is ridiculous and totally uninformative. Let $ f$ be the function which accepts as input the date of California Super Lotto drawings, and returns the set of winning numbers for that date. For instance, we could define almost anything we want in terms of functions. Given some input, produce the appropriate output.
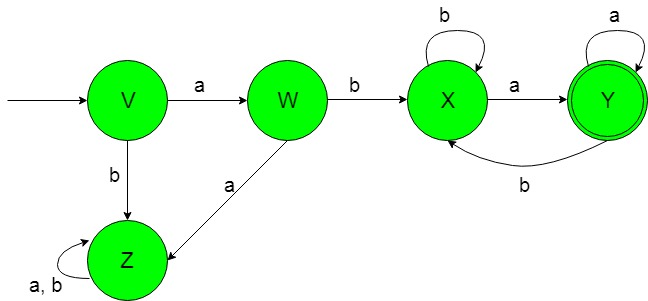
The first step in studying the sorts of possible computations (and more interestingly, those things which cannot be computed) is to define exactly what we mean by a “computation.” At a high level, this is easy: a computation is simply a function. We devote the second half entirely to Turing machines and the halting problem, but to facilitate the discussion of Turing machines we rely on the intuition and notation developed here.



 0 kommentar(er)
0 kommentar(er)
